
スポンサーリンク
※サイト運営にサーバーは必須です※
~このサイトもエックスサーバー![]() を使用しています~
を使用しています~
![]()
目次
はじめに
「サイコロの面をあてるだけの簡単なお仕事」というアプリをリリースする際に、サイコロの回転パターンを真面目に考える必要があった。
その時の経験をもとに、この記事では、最小の回転数(5回分)でサイコロの6面全部を通る場合の数を考える。
※以下のようなケースは排除して考える
「↑」「↑」「↑」「→」「↑」「↑」
例えば、最初に同じ方向に3回回った状況下で、次に別の面を進むには、右側に90度回るか、左側に90度回るかの2パターンある。しかし、その次で今までに通ったことのない面に進もうとしても、どの面も通ったことがある面となる。つまり、最小の回転数で全面を網羅するパターンに該当しない。
いきなり結論
答えは、40通り(私が計算ミスをしていない限り)
考え方1:普通に考える
まず、最初の1回目の回転は、「↑」「→」「↓」「←」の4つの好きな方向に進める。
ここでは、最初に「↑」を選んだとする。
2回目の回転は、「↓」以外の「↑」「→」「←」の3通りが考えられる。
しかし、「↑」を選ぶ場合と、「→」「←」を選ぶ場合とで場合分けが生じる。
[1]2回目も「↑」の場合
3回目も「↑」を選ぶと、途中で詰むので、3回目は「→」「←」かの2通り。その後は、1通りに定まる(「↑」、「↑」)
[2]2回目が「→」「←」の場合
3回目で進める方向は2つあるので、2通り。
4回目でも進める方向は2つあるので、2通り。
5回目は自動的に定まるので1通り
以上をまとめると
4×(1×2×1×1+2×2×2×1)=40通り
考え方2:展開図で考える
サイコロの展開図のパターンは全部で11パターン存在する。
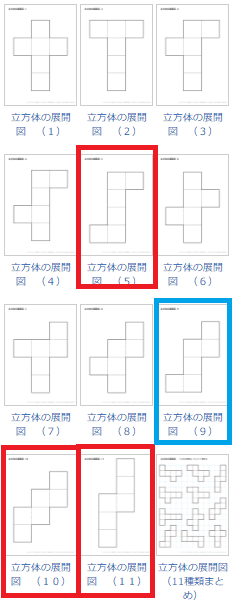
※上の図は、http://happylilac.net/zukei-rippotaitenkaizu.html
から借りてきている。(自分で一から作成するのは骨が折れるので……)
11通りある中で、一筆書きできるパターンはわずか4通り。(赤色か青色で囲まれている)
5、9、10、11の4つ。
ここで、9番目のパターンだけは、点対称ではない(図形の真ん中に画びょうを指して、180度回転させても一致しない)。そこで、このパターンを9´と呼ぶ。
5、9、9´、10、11(全部で5通り)
次に、これらの線対称の図形を考える(図形を裏側にひっくり返すことに対応する)
元の図形と、線対称の図形は、回転を考える場合にはべつものと考える必要がある。
5通り×2通り
※例えば、9番目のパターンの場合
(元の図形)「→」「↑」「↑」「→」「↑」「←」
(線対称の図形)「←」「↑」「↑」「←」「↑」
最後に図形全体を90度回したものも、回転を考えた時には、別個のものと扱う必要がある。これは、最初の一回目の回転で、「↑」「→」「↓」「←」の好きな方向を選べる自由度に相当する。
5通り×2通り×4通り=40通り
関連記事
アプリを作った時に自作した、サイコロの画像を無料で公開している。
必要な方はぜひ、気軽に使用してください
「サイコロの面をあてるだけの簡単なお仕事」のダウンロードページ:https://play.google.com/store/apps/details?id=com.kaen.dice
~プログラミングを勉強してみませんか?~
TechAcademy [テックアカデミー] ![]() は無料の体験講座が用意されているので、気軽に体験できます。
は無料の体験講座が用意されているので、気軽に体験できます。
※私(サイト主)も無料体験講座を実際に受けてみました(→感想)






コメント