同じ誕生日のペアがどのくらいいるかシミュレーション

※サイト運営にサーバーは必須です※
～ロリポップ！はコスパのよい初心者向けサーバーです～

はじめに

「同じ誕生日のペアがどのくらいいるかシミュレーション」という名前のAndroidアプリをリリースした。

内容的には、Windows用に以前作った「Birthday_Simulator」とほぼ同じ。

「Birthday_Simulator」という名前がイマイチな気がしたので、アプリの名前を変えた。

少し名前が長ったらしい気もするが、意味が伝わらないよりましだろう……

※「Birthday_Simulator」のダウンロードページは、誕生日シミュレーションソフト「Birthday_Simulator」(無料)

※「同じ誕生日のペアがどのくらいいるかシミュレーション」(Google Play のアプリ紹介ページ）：https://play.google.com/store/apps/details?id=com.kaen.birthday_simulator&hl=ja

何ができるの？

同じ誕生日のペアがどのくらいいるかシミュレーションすることができる。

計算にはモンテカルロ法を用いている。

うるう年を含む場合と含まない場合の両方を計算可能。

例えば、以下のようなことを知ることができる

100人の中に同じ誕生日の組は何組いるか？→約11.35323組

自分を含めて、100人の集団で、自分と同じ誕生日の人が自分を含めて3人以上いる確率→約2.76％

※このアプリは、乱数を用いた数値的に算出している。解析的な答えではないので、誤差が存在する。

実行するとこんな感じの画面になる

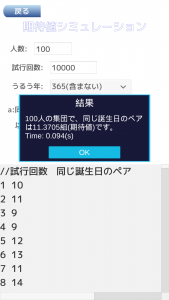
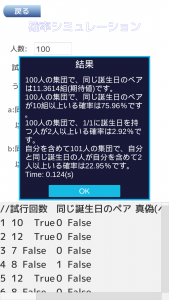
一応、英語対応させている。

英語の方の名前は「Same Birthday Pairs Simulator」

※英語の成績が芳しくなかった私が、Google翻訳を駆使しながら、適当に英訳。ミススペルや文法的なミスがゴロゴロありそう。

説明書

アプリに添付している説明書を一応ここにも載せておく

[このアプリでできること]

　同じ誕生日のペアがどのくらいいるかシミュレーションすることができる。

　計算にはモンテカルロ法を用いている。

　うるう年を含む場合と含まない場合の両方を計算可能。

　例えば、以下のようなことを知ることができる

　100人の中に同じ誕生日の組は何組いるか？→約11.35323組

　自分を含めて、100人の集団で、自分と同じ誕生日の人が自分を含めて3人以上いる確率→約2.76％

[使用上の注意点]

　このアプリは、乱数を用いた数値的に算出している。解析的な答えではないので、誤差が存在する。

　オバーフローに注意。大きすぎる数字を扱うとアプリが止まる危険性がある。

　このアプリの作成にはUnityを使用している。Unityの仕様の関係上、1万5千字を超える文字列を一遍に扱えない。
　そのため、下窓に表示される計算結果は、1万4千字を超えた時点で、表示を打ち止めするようにしている。

　誤差を少なくするためには、試行回数を増やさないといけない。しかし、試行回数を増やすと、処理が終わるまでの時間が長くなる。

※今どれくらい処理が終わったか表示する機能はない。試行回数を10倍にすると、プログラムの処理が終わる時間もおよそ10倍になる。
　そこで、まずは、試行回数を少なめにして、計算する。結果の一番後ろに、どれだけ時間(Time)がかかったか記録される。この測定時間をもとに、どれだけ、処理に時間がかかるか見積もることができる。

[アルゴリズム]

　はじめに、365（うるう年を含める場合は366）の配列を用意する。

　その後、1～365の乱数を集団の人数分だけ振る。

　例えば1の数字が出たら、1/1（１日目）に誕生日を持つ人がいると考えている。

　うるう年の場合は、1～365.25までの乱数を振って、365～365.25の範囲に入った場合にカウントするようにしている。

※より正確に言えば、振っている乱数は1～365(365.25)でなく、1～366(366.25)である。生成した実数の乱数が1以上2未満(切り捨てして1になる場合)に1と判定しているため。

※うるう年の処理の仕方が微妙に違うが、私の運営するホームページにシミュレーションコードを置いてある。このソフトはC#で書いているが、ホームページで書いているソースコードはC（C++）言語に対応。

[モードの説明(共通部)]

　5つのシミュレーションモードが存在するので、どれか1つ選ぶ。下に行くほど時間のかかる処理をしている。

1：個別シミュレーション（試行回数1）

　試行回数が１回なので、このシミュレーションの需要はほぼないと思う。期待値シミュレーション以降のシミュレーションは、この個別シミュレーションを何度も回しているので、動きの確認用としての意味合いが強い。

　366日目がうるう年に対応していると考えている。

　条件aで指定した人数より多い場合、Trueと表示される。

2：期待値シミュレーション（試行回数指定可）

　個別シミュレーションを複数回行い、ある数の集団の中、同じ誕生日の組は何組いるかを計算。個別シミュレーションの上位版。

3：確率シミュレーション（試行回数指定可）

　個別シミュレーションを複数回行い、ある数の集団の中、同じ誕生日の組は何組いるかを計算。また、それにまつわる確率も計算。期待値シミュレーションの上位版。

　うるう年を含む場合、「試行回数」「同じ誕生日のペア」「真偽(ペア)」「1/1の人数」「真偽(1/1)」「2/29の人数」「真偽(2/29)」の7つの項目が表示される。

・「真偽(ペア)」：「同じ誕生日のペア」が条件bで指定された組より多かった場合、True。

・「1/1の人数」：1/1に誕生日を持つ人数

・「真偽(1/1)」：「1/1の人数」が条件aで指定された人数より多かった場合、True。

　「2/29の人数」「真偽(2/29)」も1/1の場合と同様に考える。

4：人数vs期待値（指定した人数の範囲で期待値シミュレーションを行う）

　期待値シミュレーションを複数回行う。期待値シミュレーションではできなかった、集団の人数の範囲指定ができる。人数vs同じ誕生日の組(期待値)をプロットする際に有用。期待値シミュレーションの上位版。

5：人数vs確率（指定した人数の範囲で期待値シミュレーションを行う）

　確率シミュレーションを複数回行う。確率シミュレーションではできなかった、集団の人数の範囲指定ができる。人数vs確率をプロットする際に有用。確率シミュレーションと人数vs期待値の上位版に相当。

　「人数」「同じ誕生日のペア(期待値)」「ペアのいる確率(％)」「1/1のペア確率(％)」「自分と同じ誕生日の確率(％)」「2/29のペア確率(％)」「自分と同じ誕生日の確率(2/29)(％)」の7つの項目が表示される。

　何を意味しているか分かりづらい場合は、「3：確率シミュレーション」を実行してみる。「5：人数vs確率」は、人数を変えながら、「3：確率シミュレーション」の最終結果を表示しているようなもの。

　「同じ誕生日のペア(期待値)」:ある人数の集団において、同じ誕生日のペアの組がどれだけいるか期待値を算出

・「ペアのいる確率(％)」:ある人数の集団において、条件bで指定した以上の組が存在する確率。

・「1/1のペア確率(％)」:ある人数の集団において、1/1に誕生日を持つ人が条件aで指定した人数以上いる確率。

・「自分と同じ誕生日の確率(％)」: ある人数の集団に対して、自分と同じ誕生日の人が自分を含めて(条件aで指定した人数)以上いる確率。1月１日(1日目の人数)に同じ誕生日の人数が(条件aで指定した人数－1)人以上いる状況を考えて判定している。

・「2/29のペア確率(％)」：ある人数の集団において、うるう年の人が条件aで指定した人数以上いる確率。

・「自分と同じ誕生日の確率(2/29)(％)」：ある人数の集団に対して、自分がうるう年に生まれていると仮定して、自分を含めて(条件aで指定した人数)以上いる確率。2月29日に同じ誕生日の人数が(条件aで指定した人数－1)人以上いる状況を考えて判定している。

[条件の指定]

　条件が不適当だった場合、自動修正される。

・人数：現在考えている集団の人数を指定(2以上の整数を指定)

・試行回数：個別シミュエーションを行う回数。デフォルトでは千回になっている。誤差を少なくしたいなら、試行回数を増やす必要がある。時間がかかるようなら減らす。(1以上の整数を指定)

・うるう年：「含む」か「含まない」か選択することができる。

・条件a「同じ誕生日の人が「x」人以上いる時、1組とカウント」：特別な理由がないのであれば2のままにする。特殊な状況でなければ、2人いれば、同じ誕生日のペアが１組あるとカウントすると思われる。例えば、100人の中に3人が同じ誕生日の確率を求めたいのであれば2でなく3にする必要が出てくる。(2以上の整数を指定)

・条件b「同じ誕生日の組が「x」組いる時の確率を求める」：例えば、100人の中に同じ誕生日の組が10組以上いる確率を知りたい場合は「x」を「10」にする。(1以上366以下の整数を指定)

[その他注意事項]

　期待値シミュレーション及び確率シミュレーションのモードを選択して、試行回数を１万回にした場合、500～800回程度で表示が途切れる。これは、表示できる文字数の制約が１万５千字であるからだ。ただし、最終的な結果は、きちんと１万回計算したものが出力される。その点は、安心してもらいたい。

[対応プラットフォーム]

　出力した結果をテキストファイルに保存する機能は、残念ながらこのソフトにはついていない。その代りと言っては何だが、Windows上で動くフリーソフトを用意してある。名前は「Birthday_Simulator」。
　アプリの紹介ページで、私のホームページへのリンクがあるはずなので、そこからたどることができる。

～ギャンブルに絶対儲かる必勝法があるのだろうか？～

私(サイト主)はこの疑問に対して非常に興味を持ち、プログラミングで検証してみました。

このサイトを応援してもいいかなと思う人はぜひとも購入を検討してみてください。

ギャンブルの必勝法が本当に儲かるかプログラミングで検証してみた