同じ誕生日の組がどれだけ存在するか？適当に見積もってみる

はじめに

※追記：完成したアプリの紹介→同じ誕生日のペアがどのくらいいるかシミュレーション

昔、ある組織に所属しており、イベント用の問題を作らないといけなかった。

そこで私が、同じ誕生日の人が何組あるかという問題を思いついた。

名簿上は120人ほどの集まりであった。

同じ誕生日の人って結構レアだし、当初は、せいぜい10組程度だろうと高をくくっていた。

だが、数えてみると20組近くもいた。

120人という集団の中で、20組ということは、40人がだれかと同じ誕生日の人がいるということ。

想像以上の人数に驚いた
そして、個人的な直観と外れて、なんでだろうなと思っていた。

ある数の中に何組同じ誕生日の人間がいるか？という問題

ルール：同じ誕生日の人がいた場合1組と数え、たとえ3人以上が同じ誕生日でも、1組とカウントするとする。

少ない人数の集団だと0組で、たくさんの数を集めると365組（うるう年を考えると366組）

ここで、なぜ120人の中に20組も同じ誕生日の人がいたか自分なりに考えてみた

ざっくりした見積もり

※以下の考え方はだいぶ適当。365人を超えると直観的にあまり正しくなくなる
ほどほどの人数の時にしか正しく機能しないと思われる

例えば120人だとする。

ある一人に注目する。

自分以外の人間が約120人（正確には119）いる。この中に自分と同じ誕生日の人がいる期待値はだいたい

120/365（正確には119/365）で約1/3

この期待値に、集団に存在する人数をかけて、

1/3×120＝40人ほどが同じ誕生日。

40人ということは20組に相当する。（いわゆるダブルカウントの分1/2する）

中間的な人数の場合、人数がN人としたら
N×（N-１）/（365×2）でだいたい見積もれるのではないかな……

※検索するとまじめに漸化式でサイトもあるが、このサイトはそこまでガチではない

それと現実には、特定の誕生日に人が集まり、逆にある誕生日には人が集まらない。

例えば年始である1/1が避けられる。
逆に、学年の区切りとなる4/2は好まれたりする

このように、実際問題として、誕生日のかたよりが生じる。

グラフ（追記）

N×（N-１）/（365×2）の式とプログラムを作ってシミュレーションした人数VS誕生日が同じペア（組）：うるう年なしバージョンの結果を比べてみる

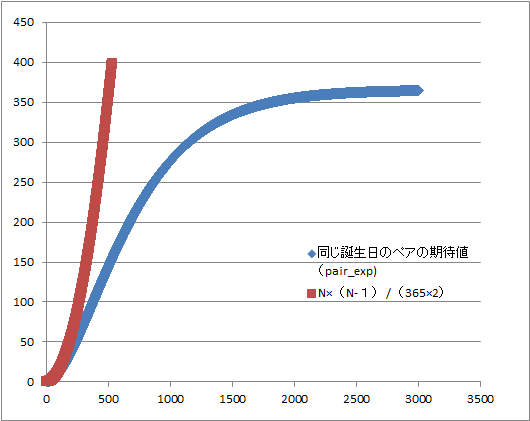
N×（N-１）/（365×2）の式は、シミュレーションの結果よりもだいぶ高く評価される傾向にある。

例えば、124人の段階で、シミュレーションと比較して、N×（N-１）/（365×2）の式の結果は3割ほど多い人数となる。

また、206人の段階で、シミュレーションと比較して、N×（N-１）/（365×2）の式の結果は5割ほど多い人数となる。

100人以下なら、N×（N-１）/（365×2）の式の見積もりはまだ使えるかなといった感じ

エクセルファイル（結果）のダウンロード：simulation_k100000_d366-compare.xlsx

※ちなみに、120人の場合、誕生日が同じペアの期待値（シミュレーション）は15.80878組。120人の集団に20組の誕生日の組がいるというのは、だいぶ多いケースにあたる

関連記事

※追記：完成したアプリの紹介→同じ誕生日のペアがどのくらいいるかシミュレーション

• 同じ誕生日の組がいくついるか数えるプログラムの方針